Tree
这里是深度优先遍历,广度优先遍历看这个Note
一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果
前序位置的代码执行自上向下,后序位置的代码执行自下向上的
方法:
遍历一遍二叉树: 如果可以,用一个 traverse 函数配合外部变量来实现
递归: 利用这个函数的返回值,分解问题
/* 二叉树遍历框架 */
void traverse(TreeNode root) {
if (root == null) return;
traverse(root.left);
traverse(root.right);
}
/* 多叉树遍历框架 */
void traverse(Node root) {
if (root == null) return;
for (Node child : root.children)
traverse(child);
}
/* 图遍历框架 */
boolean[] visited;
void traverse(Graph graph, int v) {
// 防止走回头路进入死循环
if (visited[v]) return;
// 前序遍历位置,标记节点 v 已访问
visited[v] = true;
for (Vertex neighbor : graph.neighbors(v))
traverse(graph, neighbor);
}
Max Depth of Tree
int depth = 0;
int maxD = 0;
int maxDepth(TreeNode root) {
traverse(root);
return maxD;
}
void traverse(TreeNode input){
if(input == null){
return;
}
depth++; // came to the next level, accumulate depth
if(input.left == null && input.right == null){ // reach leaf node, this is the base case
maxD = Math.max(maxD, depth);
}
traverse(input.left);
traverse(input.right);
depth--; // left a level and went to the other branch of input's parent, unregister depth because we came up a level
}
Diameter of tree
int max = 0;
public int diameterOfBinaryTree(TreeNode root) {
maxDepth(root);
return max;
}
int maxDepth(TreeNode root){
if(root == null){
return 0;
}
int leftmax = maxDepth(root.left);
int rightmax = maxDepth(root.right);
int diameter = leftmax + rightmax;
max = Math.max(diameter, max);
return 1 + Math.max(leftmax, rightmax);
}
invert binary tree
public TreeNode invertTree(TreeNode root) {
if (root == null){
return root;
}
// 这里使用递归来处理每一次的交换所用到的值,默认其已经完成了反转
TreeNode right = invertTree(root.right);
TreeNode left = invertTree(root.left);
// 这里就不需要考虑逻辑,只需要写出来我希望把左右交换就行
root.right = left;
root.left = right;
return root;
}
flatten tree
public void flatten(TreeNode root) {
if(root == null){ // base case
return;
}
// flatten left and right
flatten(root.left);
flatten(root.right);
TreeNode right = root.right;
TreeNode left = root.left;
// use right as next, hence left is now null
root.left = null;
root.right = left;
// create a dummy head to preserve the root
TreeNode dummy = root;
while(dummy.right != null){ // traverse to the end of the head+left list
dummy = dummy.right;
}
dummy.right = right; // add right to the end of list
}
maximum tree
public TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums, 0, nums.length-1);
}
TreeNode build(int[]nums, int left, int right){
if(right < left){ // base case
return null;
}
// find max and it's pointer
int max = Integer.MIN_VALUE;
int pointer = -1;
for(int i = left; i <= right; i++){
if(nums[i] > max){
max = nums[i];
pointer = i;
}
}
TreeNode root = new TreeNode(max);
root.left = build(nums, left, pointer - 1); // parse the left
root.right = build(nums, pointer + 1, right); // parse the right
return root;
}
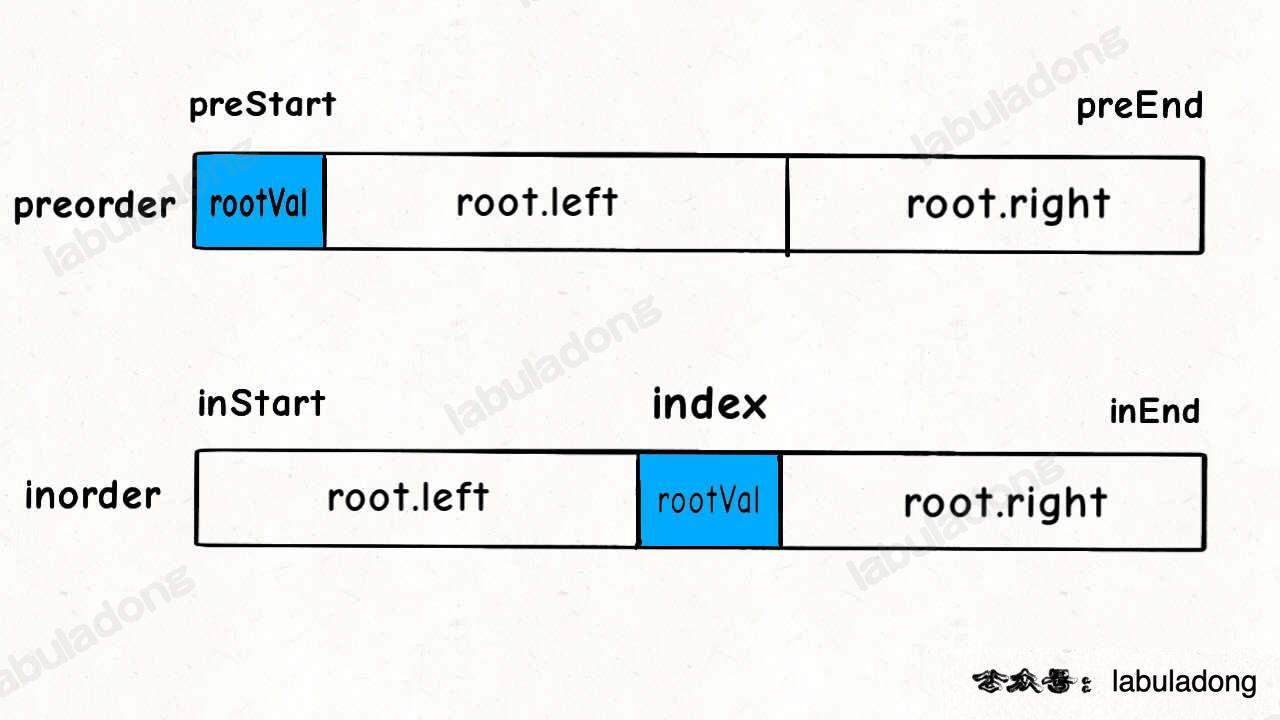
tree from preorder/inorder
HashMap<Integer, Integer> valToIndex = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
for (int i = 0; i < inorder.length; i++) { // 放入hashmap方便读取
valToIndex.put(inorder[i], i);
}
return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
}
TreeNode build(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {
if (preStart > preEnd) { // basecase
return null;
}
int rootVal = preorder[preStart]; // root 节点对应的值就是前序遍历数组的第一个元素
int rootindex = valToIndex.get(rootVal); // rootVal 在中序遍历数组中的索引, 以此来分割inorder序列
int leftSize = rootindex - inStart;
TreeNode root = new TreeNode(rootVal);
root.left = build(preorder, preStart + 1, preStart + leftSize, inorder, inStart, rootindex - 1);
root.right = build(preorder, preStart + leftSize + 1, preEnd, inorder, rootindex + 1, inEnd);
return root;
}
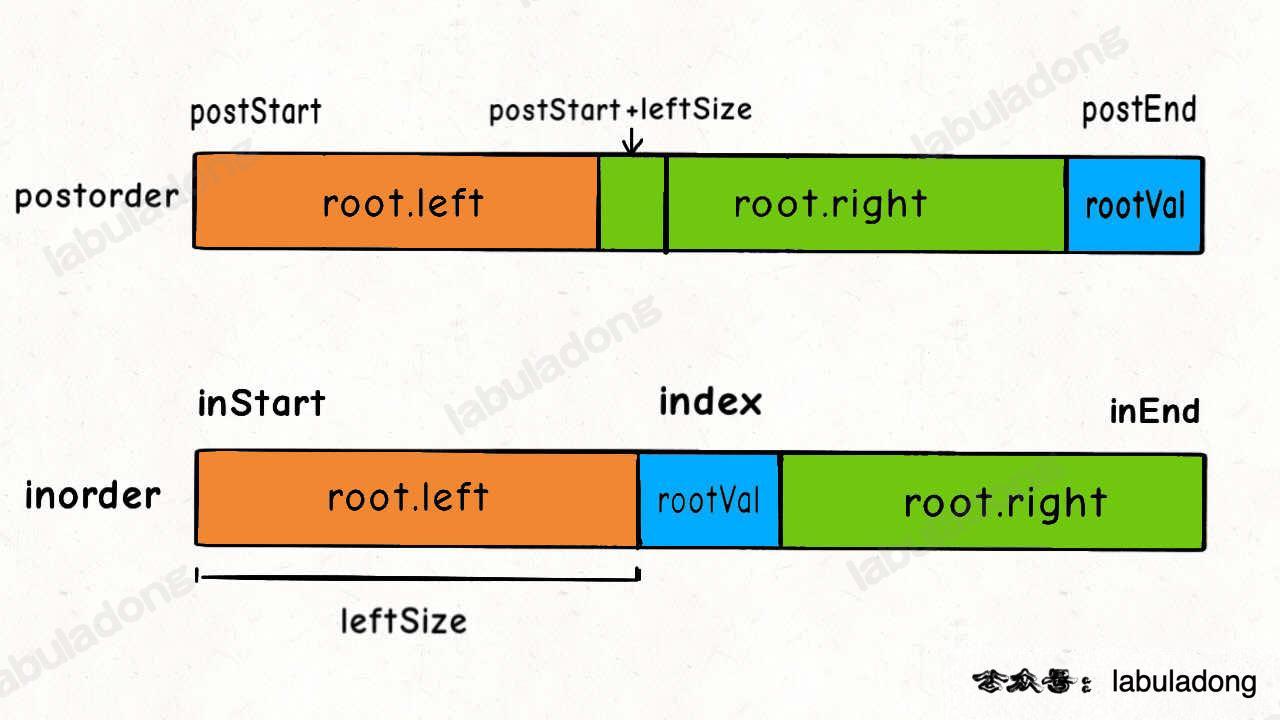
tree from inorder and postorder
HashMap<Integer, Integer> valToIndex = new HashMap<>();
public TreeNode buildTree(int[] inorder, int[] postorder) {
for (int i = 0; i < inorder.length; i++) { // 放入hashmap方便读取
valToIndex.put(inorder[i], i);
}
return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
}
TreeNode build (int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd){
if (inStart > inEnd) { // base case
return null;
}
int rootVal = postorder[postEnd];
int rootIndex = valToIndex.get(rootVal);
TreeNode root = new TreeNode(rootVal);
root.left = build(inorder, inStart, rootIndex-1, postorder, postStart, postStart + rootIndex - inStart - 1);
root.right = build(inorder, rootIndex + 1, inEnd, postorder, postStart + rootIndex - inStart, postEnd - 1);
return root;
}
tree from preorder and postorder
HashMap<Integer, Integer> valPointer = new HashMap<>();
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
for(int i = 0; i < postorder.length; i++){
valPointer.put(postorder[i], i );
}
return build(preorder, 0, preorder.length-1, postorder, 0 , postorder.length-1);
}
TreeNode build(int[]preorder, int preStart, int preEnd, int[]postorder, int postStart, int postEnd){
if(preStart > preEnd){ // tree的叶节点
return null;
}
if (preStart == preEnd) { // basecase
return new TreeNode(preorder[preStart]);
}
int rootVal = preorder[preStart];
TreeNode root = new TreeNode(rootVal);
int leftRootVal = preorder[preStart + 1]; // 从preorder里找到左的root值,去map查index
int index = valPointer.get(leftRootVal);
int leftSize = index - postStart + 1; // 左子树的元素个数
root.left = build(preorder, preStart + 1, preStart + leftSize, postorder, postStart, index);
root.right = build(preorder, preStart + leftSize + 1, preEnd, postorder, index + 1, postEnd - 1);
return root;
}
serialize/deserialize
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb = new StringBuilder();
serialize(root, sb);
return sb.toString();
}
void serialize (TreeNode root, StringBuilder sb){
if(root == null){
sb.append("#").append(",");
return;
}
sb.append(root.val).append(",");
serialize(root.left, sb);
serialize(root.right, sb);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
LinkedList<String> nodes = new LinkedList<>();
for (String s : data.split(",")) {
nodes.addLast(s);
}
TreeNode result = deserialize(nodes);
return result;
}
public TreeNode deserialize(LinkedList<String> nodes) {
if (nodes.isEmpty()) return null;
// 左侧=根节点
String first = nodes.removeFirst();
if (first.equals("#")) return null;
TreeNode root = new TreeNode(Integer.parseInt(first));
root.left = deserialize(nodes);
root.right = deserialize(nodes);
return root;
}
find duplicate subtrees
HashMap<String, Integer> memo = new HashMap<>(); // 记录所有子树以及出现的次数
ArrayList<TreeNode> result = new ArrayList<>(); // 记录重复的子树根节点
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
traverse(root);
return result;
}
String traverse(TreeNode root) {
if (root == null) {
return "#";
}
String left = traverse(root.left);
String right = traverse(root.right);
String subTree = left + "," + right + "," + root.val;
int freq = 0; // if the subtree dose not exists, freq is 0
if(memo.containsKey(subTree)){
freq = memo.get(subTree);
}
if (freq == 1) { // 确保结果集不重复
result.add(root);
}
memo.put(subTree, freq + 1); // 出现次数加一
return subTree;
}